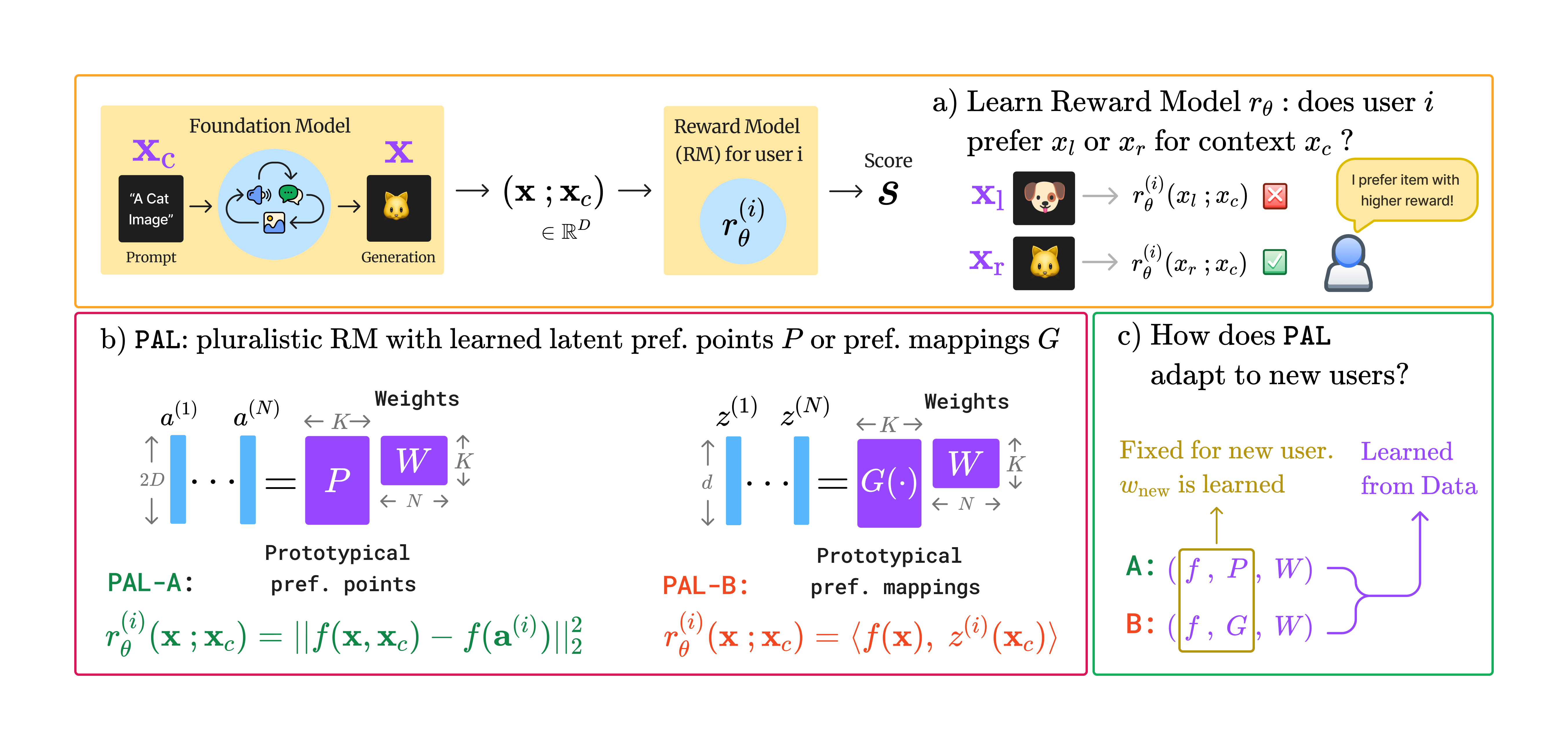
Foundation models trained on internet-scale data benefit from extensive alignment to human preferences before deployment.
However, existing methods typically assume a homogeneous preference shared by all individuals, overlooking the diversity inherent in human values.
In this work, we propose a general reward modeling framework for pluralistic alignment (PAL), which incorporates diverse preferences from the ground up.
This approach not only addresses the limitations of traditional alignment methods but also offers several key advantages that make it particularly efficient for handling diverse human preferences:
Diverse Preference Alignment: PAL can handle diverse human preferences rather than assuming a single, universal preference, addressing the variability in individual values.
Higher Performance with Fewer Parameters: e.g. for a T2T task, PAL is 1.7% more accurate for seen users and 36% more accurate for unseen users, with 20× fewer parameters.
Modular Design: PAL's architecture is modular, allowing it to leverage shared common preferences while adapting to specific individual preferences.
Few-shot Generalization: PAL enables quick adaptation to new users' preferences with few examples, making it more efficient for personalized alignment.
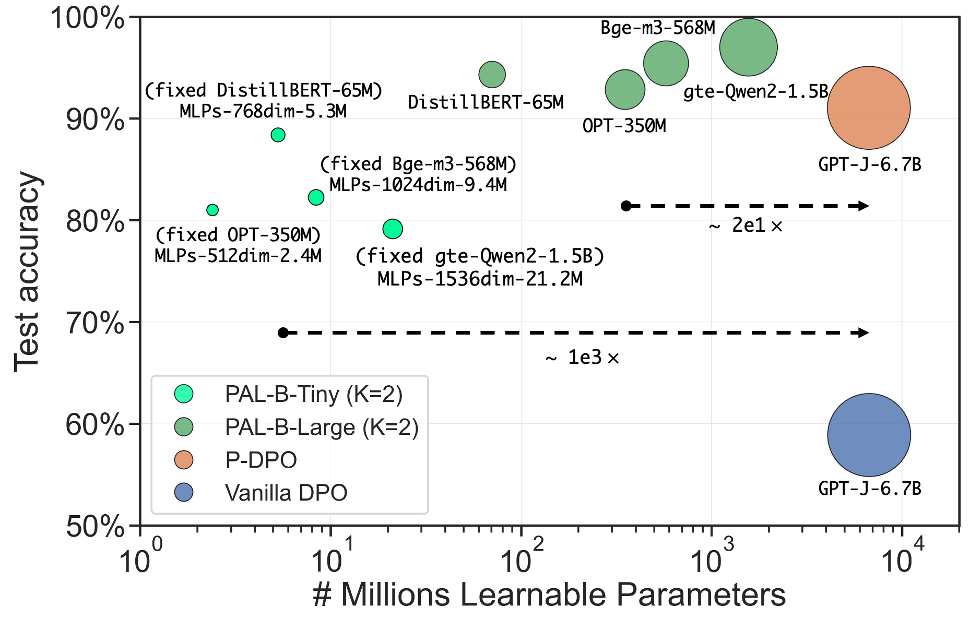
PAL is accuracy-compute optimal and shows state-of-the-art (SoTA) performance.
What is Ideal Point Model ?
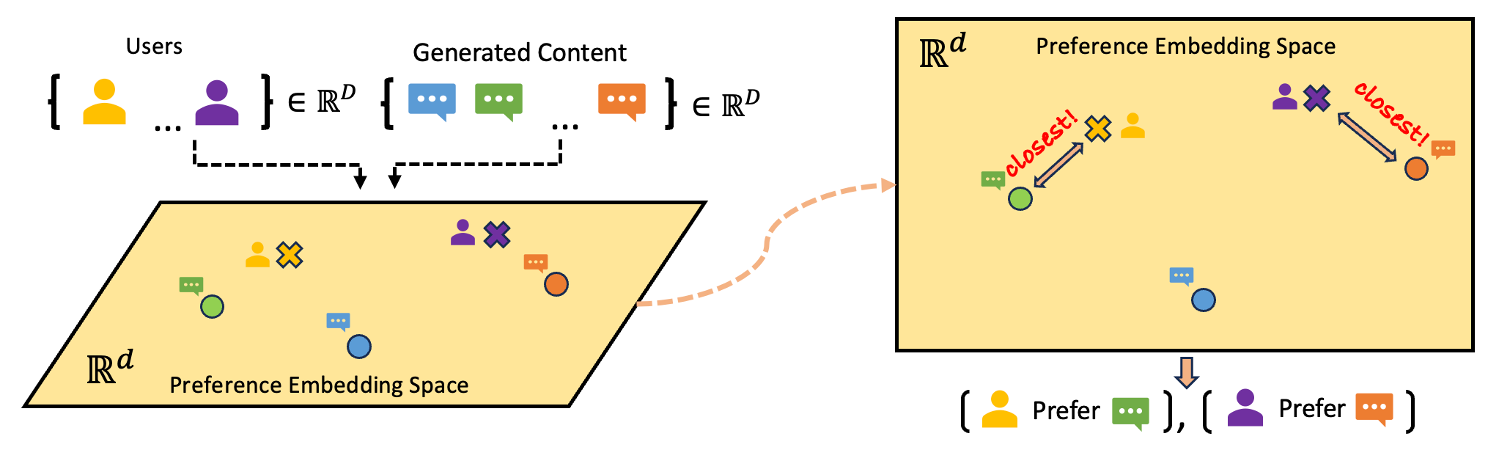
The ideal point model (Coombs, 1950) is a statistical model that is used to analyze the preferences of individuals or groups. It is broadly used in political science, sociology, and economics to model the preferences of voters, legislators, or other decision-makers. The ideal point model assumes that each individual has an "ideal point" in some high-dimensional space \(\mathbb{R}^d\), and that the individual's preference for a particular alternative is a function of the distance between the alternative and the individual's ideal point. The ideal point model is well suited for heterogeneous preference learning, which we discuss below.
PAL: Mixture Modeling for Heterogeneous Preferences
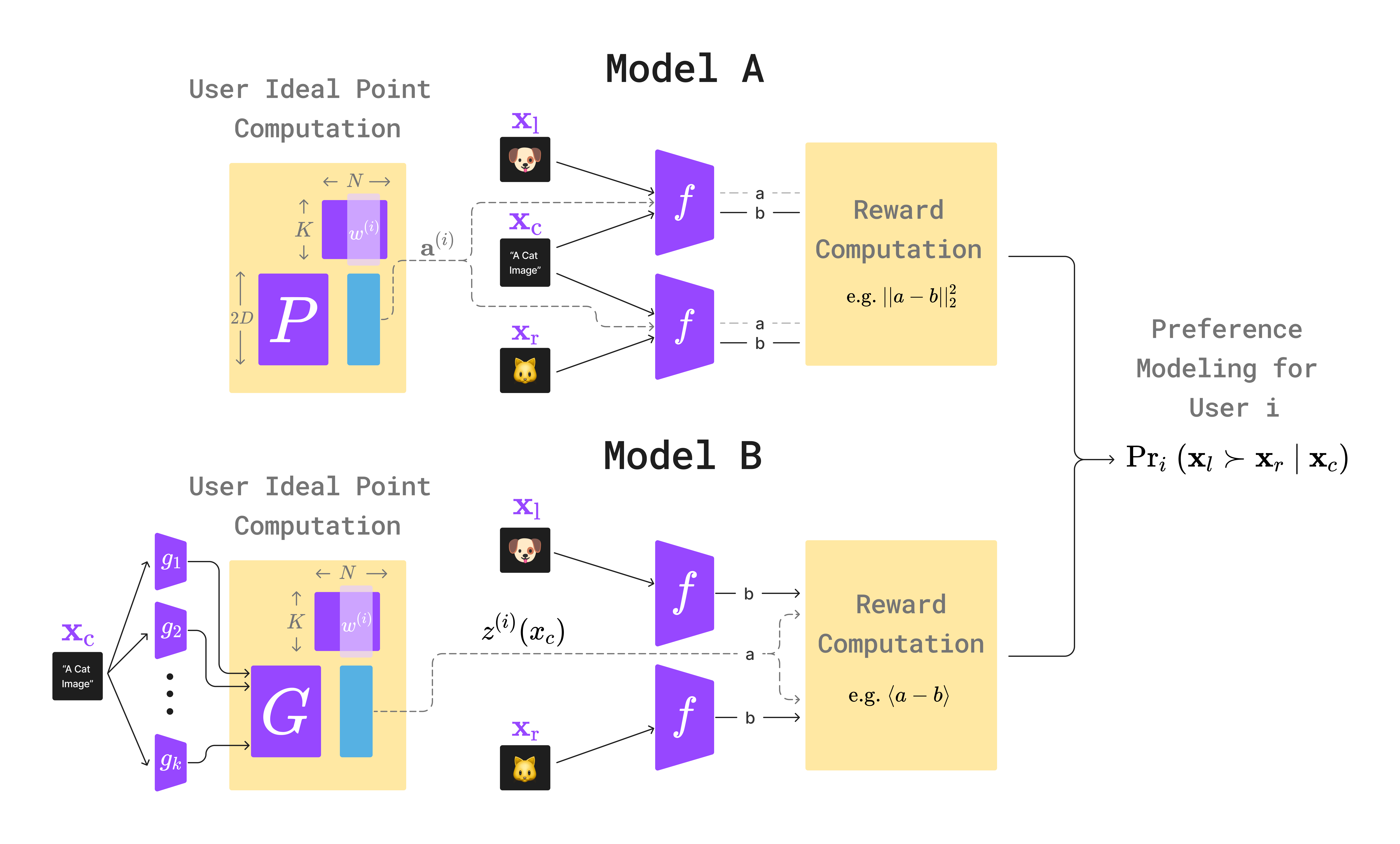
In reality, different people can have different preferences that are not just noisy perturbations of a universal model, i.e. people can differ in systematically different ways! People's preferences are not completely unique - there are shared aspects of preferences within subgroups of people, for example owing to similar demographics and educational, socio-cultural, or other types of similarities. PAL is designed to suit this structure of human preferences - in particular, we use a mixture modeling approach to capture diverse individual preferences across \(K\) subgroups, where each user's preference (ideal point) is a convex combination of:
Here the \(K\) prototypes represent the shared structure across subpopulations, while each users' weights \(W\) over the prototypes represent their individuality.
Experiments on Heterogeneous Preference Datasets
The TL;DR Summary dataset contains a series of preferences over summaries generated by language models.
For each pair of summaries, a labeler determines which one is preferred or not.
We used the variant of the TL;DR dataset proposed by Li et al., 2024, which uses the summary length as the preference.
The majority group prefers longer summaries while the minority prefers shorter summaries.
Performance:
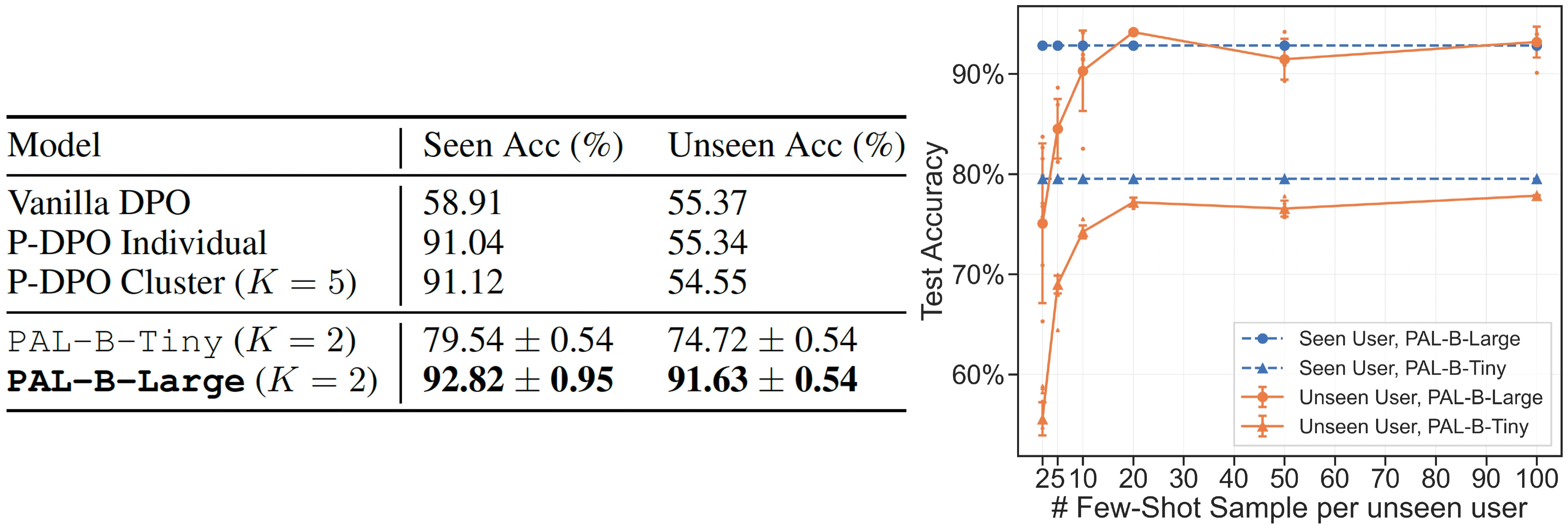
The table reports the performance of PAL-B-Large (OPT-350M) compared to SoTA P-DPO.
We observe that PAL, with around 6.3 billion fewer parameters, is \(1.7\%\) more accurate on seen users, and \(36\%\) more accurate on unseen users.
The figure illustrates PAL's ability to generalize effectively to unseen users in few-shot settings.
As the number of samples per unseen user increases, PAL progressively adapts to their preferences.
With just \(20\) samples per unseen user, PAL achieves performance comparable to that of seen users.
The Pick-a-Pic dataset is a large, open dataset for human feedback in T2I generation.
There are two versions of Pick-a-Pic, v1 and v2, where v2 extends v1.
To ensure a fair model evaluation, we divide the v2 test set into no-leakage and leakage subsets due to overlap (leakage) with the v1 train set.
We only consider the 18391 samples with no preference ties, i.e. one generated image is always preferred to the other.
Performance:
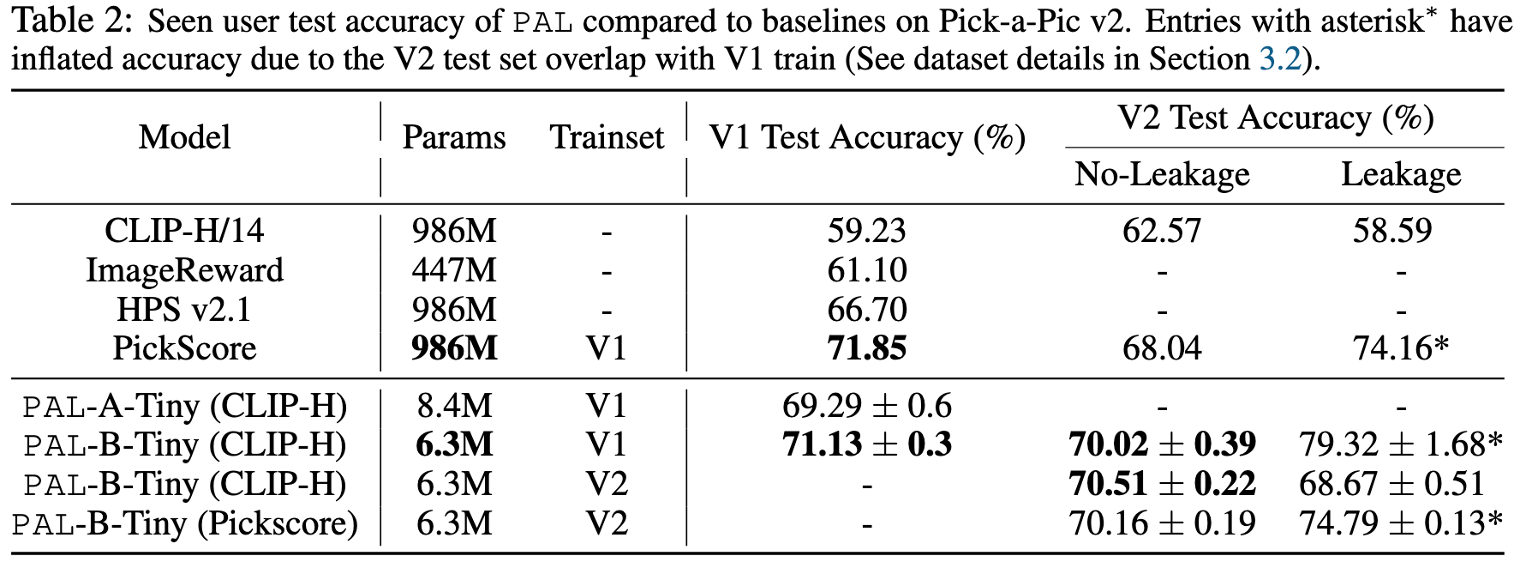
The table shows (a) PAL matches SoTA PickScore when trained on V1 with 165\(\times\) fewer parameters;
(b) PAL exceeds SoTA performance on v2-no-leakage (i.e. fair comparison) by \(2\%\) when training on v1, and by \(2.5\%\) if training on v2.
We note that PAL-B-Tiny (\(\sim\)6M params) exceeds SoTA performance while training on a single RTX 4090 GPU, whereas PickScore (\(\sim\)1B params) is trained with 8\(\times\)A100 GPUs -- highlighting the suitability of PAL for efficient and democratic reward modeling.
The Anthropic Personas dataset contains a collection of personalities or personas, each associated with 500 statements that align with the persona and 500 statements that do not.
We create a heterogeneous preference dataset by sampling pairs of persona statements and imitating the preference choices of subpopulation groups with diverse personality preferences.
Results:
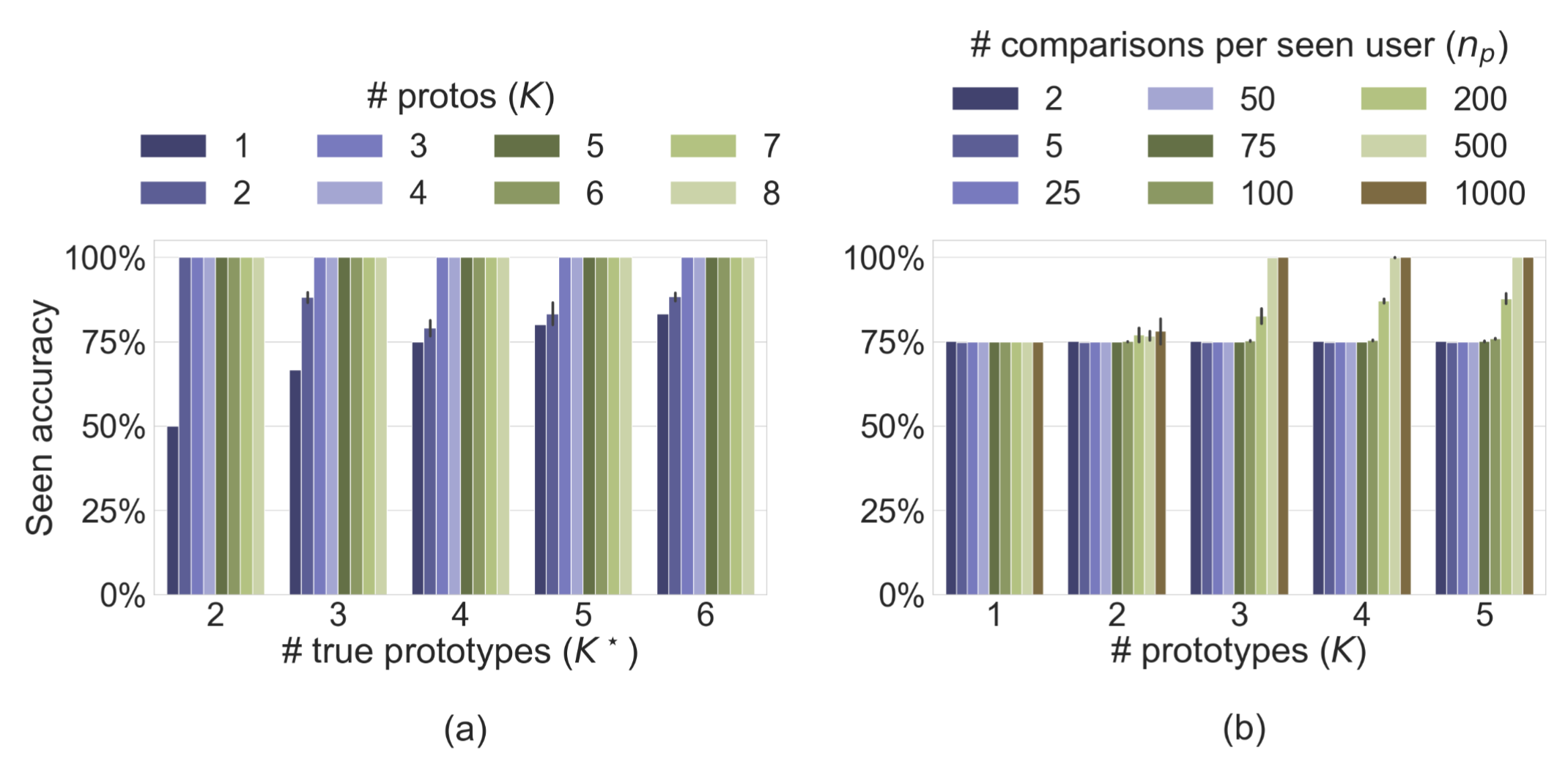
(a) On the heterogeneous persona dataset, we observe that as # learned prototypes approach the # true prototypes, i.e. \(K \to K^\star\), the seen accuracy increases to \(100\%\) given a sufficient number of users and number of comparisons per user ; (b) As we get more comparisons per seen user \(n_p\), PAL eventually saturates to 100% accuracy ( when \(K\geq K^\star=3\))
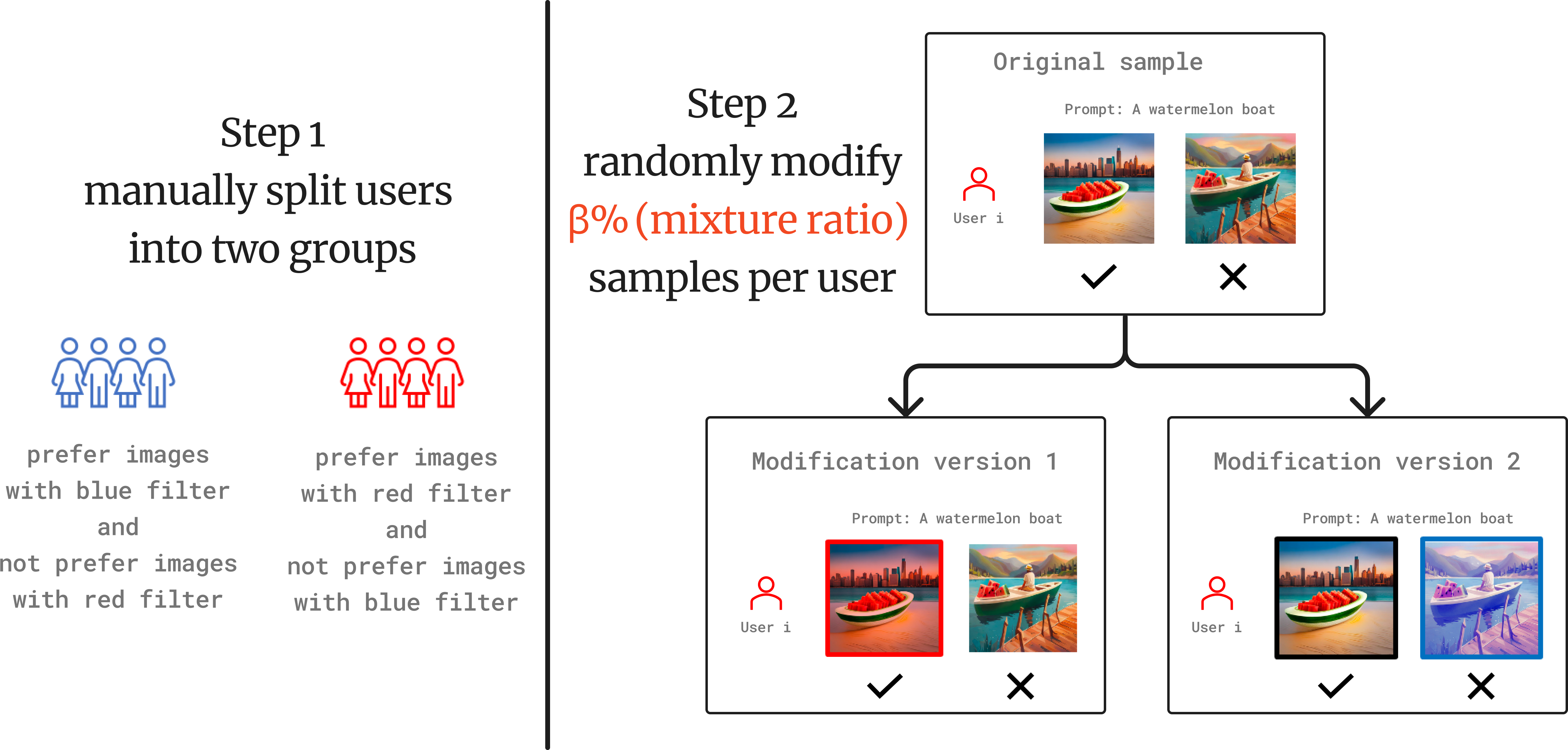
The Pick-a-Pic dataset is a large, crowdsourced open dataset of human preferences over text-to-image generation, designed to align pre-trained models with human preferences.
We construct the Pick-a-Filter dataset by assuming two subpopulation groups that prefer warm (red) or cool (blue) tones. We apply simple color filters to Pick-a-Pic V1 to semi-synthetically inject this heterogeneity.
Performance:
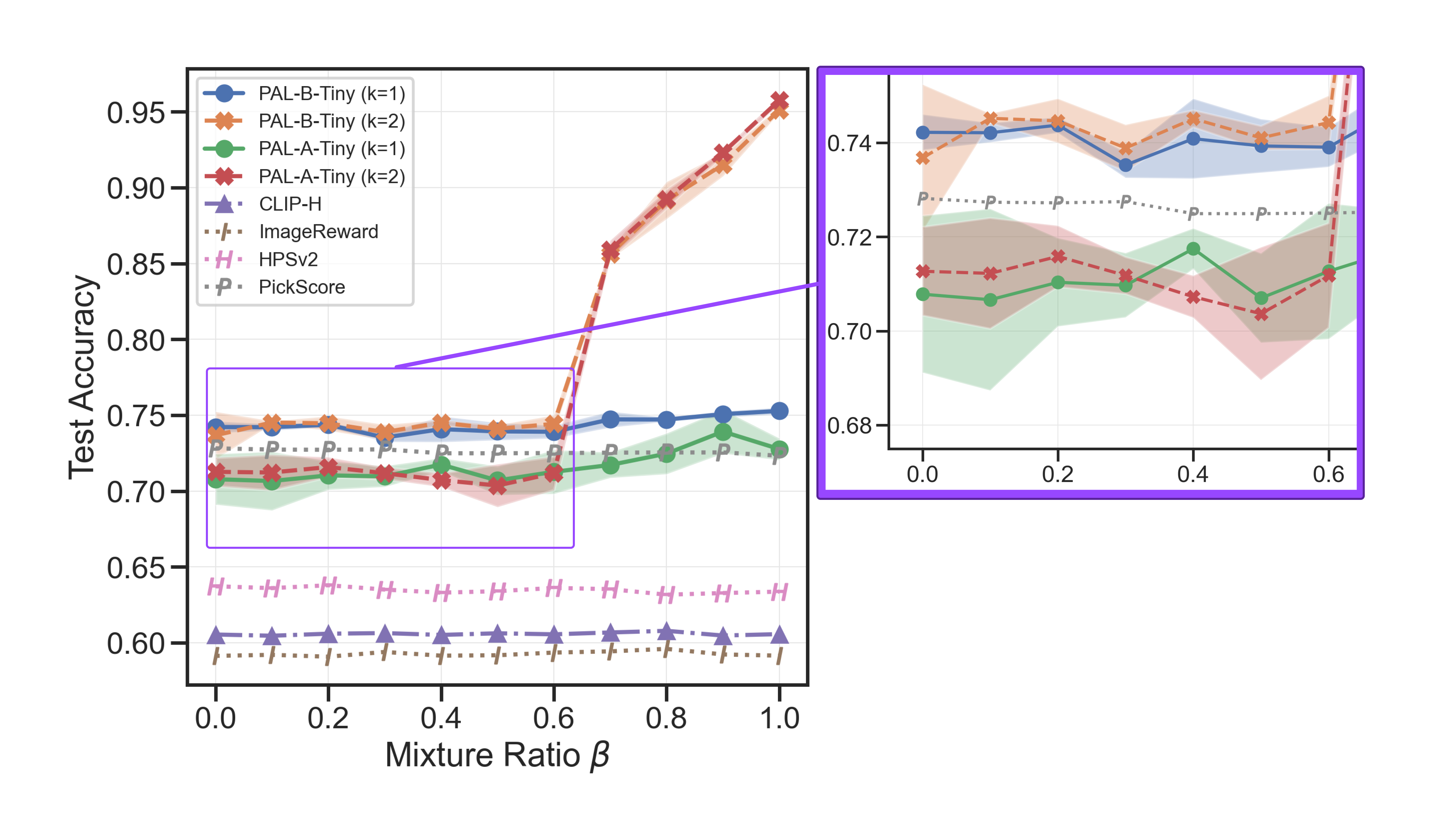
PAL enables learning beyond a universal preference \(K^* > 1\) to identify diverse user preference groups. We observe that PAL significantly outperforms the homogeneous reward model in predicting user preferences - at a mixture ratio of 1, PAL achieves \(95.2\%\) test accuracy compared to \(75.4\%\) from the homogeneous reward model (\(K=1\)).
Theoretical Guarantees and Sample Complexity
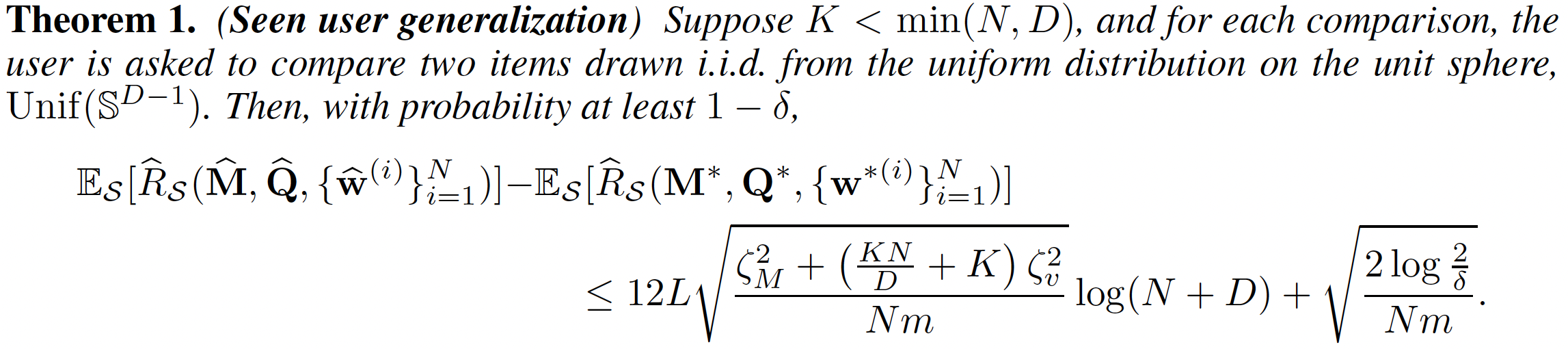
Observe that the bound decays as either the number of users \(N\) or the number of samples per user \(m\) increases. In addition, when \(N \ge \Omega(\dim x^2)\), the bound simplifies to \(\tilde{O} (\sqrt{K/m})\), which implies a per-user sample complexity of \(\tilde{O}(K)\). This contrasts with the existing result of \(\tilde{O}(D)\) without mixture modeling (Canal et al., 2022). The result captures the intuition that if the users amortize the cost of learning the common \(M\) and \(Q\), then each user only needs to individually learn their weights \(w_i \in \Delta^{K-1}\).
Intuitively, the first term captures how well the common mapping and the prototypes learned on seen users' dataset translate to new unseen users. This term decays as the number of seen users \(N\) increases. The second term characterizes how well our few-shot preference localization for a new unseen user generalizes to unseen pairs of this user. This term indicates a sample complexity of \(\tilde{O}(K)\) and suggests efficient generalization, especially since \(K\) can be quite small in practice.
Simulation Experiment: Gaussian Synthetic DatasetAssume \( K^* \) user prototypes \(\{\mathbf{p}_i\}_{i=1}^{K^*}\), where \(\mathbf{p}_i \sim \mathcal{N}(0,(1/d)I)\). We consider two settings:
1) a mixture setting, where we assume each user is located in the convex hull of \( K \) prototypes;
2) a simpler partition setting, where we assume \( N \) users are evenly sampled from \( K \) prototypes, with \(\mathbf{a}_i \in \{\mathbf{p}_k\}_{k=1}^{K}\).
Each sample is generated as follows: we randomly draw two items \(\{\mathbf{x}_l, \mathbf{x}_r\}\) and one user \(\mathbf{a}_i\), and label the user's preference as \(\text{sign}(\|f^*(\mathbf{x}_l)-f^*(\mathbf{a}_i)\|_2-\|f^*(\mathbf{x}_r)-f^*(\mathbf{a}_i)\|_2)\). We generate a total of \( n \) samples per user to learn the user's ideal point. We use model A with a single-layer MLP (without bias) with hinge loss and evaluate on the held-out test set.
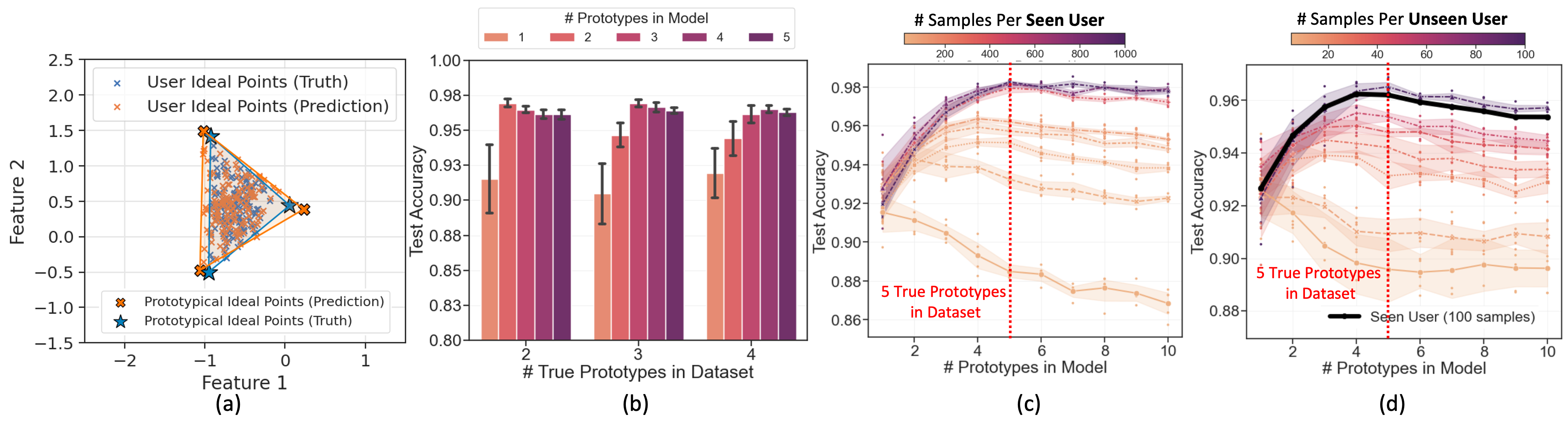
Figure (a) shows that PAL can align the user ideal points to the true user ideal points in the representation space. Figure (b) shows that the homogeneous reward model (# prototypes = 1) can only achieve sub-optimal performance on the simulated dataset when diverse preferences exist. When we learn pluralistic preferences by setting multiple learnable prototypes with PAL, we gain a significant 7% accuracy boost. Figure (c) shows that as we increase the number of training samples for seen users, PAL achieves higher test accuracy, and is also more accurate in capturing the true number of prototypes in the dataset (which we know from simulations). Figure (d) shows that even for the unseen users (new users not in the training set), PAL can effectively generalize to accurately predict preferences with fewer examples.
@misc{chen2024palpluralisticalignmentframework,
title={PAL: Pluralistic Alignment Framework for Learning from Heterogeneous Preferences},
author={Daiwei Chen and Yi Chen and Aniket Rege and Ramya Korlakai Vinayak},
year={2024},
eprint={2406.08469},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2406.08469},
}
This work was supported by NSF grants NCS-FO 2219903 and NSF CAREER Award CCF 2238876.
Usage and License Notice: The data, code and model checkpoints are intended for research use.